Quantum Wave in a Box
Published by:
Michel Ramillon
Description
Schrödinger equation solver 1D. User defined potential V(x). Diagonalization of hamiltonian matrix. Animation showing evolution in time of a gaussian wave-packet.
In Quantum Mechanics the one-dimensional Schrödinger equation is a fundamental academic though exciting subject of study for both students and teachers of Physics. A solution of this differential equation represents the motion of a non-relativistic particle in a potential energy field V(x). But very few solutions can be derived with a paper and pencil.
Have you ever dreamed of an App which would solve this equation (numerically) for each input of V(x) ?
Give you readily energy levels and wave-functions and let you see as an animation how evolves in time a gaussian wave-packet in this particular interaction field ?
Quantum Wave in a Box does it ! For a large range of values of the quantum system parameters.
Actually the originally continuous x-spatial differential problem is discretized over a finite interval (the Box) while time remains a continuous variable. The time-independent Schrödinger equation H ψ(x) = E ψ(x), represented by a set of linear equations, is solved by using quick diagonalization routines. The solution ψ(x,t) of the time-dependent Schrödinger equation is then computed as ψ(x,t) = exp(-iHt) ψ₀(x) where ψ₀(x) is a gaussian wave-packet at initial time t = 0.
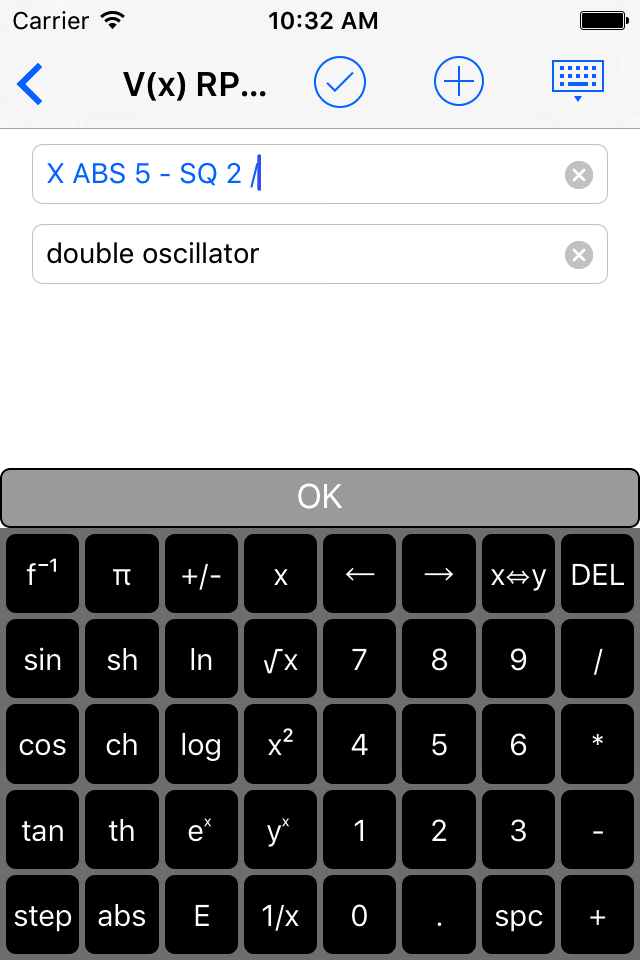
You enter V(x) as RPN expression, set values of parameters and will get a solution in many cases within seconds !
- Atomic units used throughout (mass of electron = 1)
- Quantum system defined by mass, interval [a, b] representing the Box and (real) potential energy V(x).
- Spatially continuous problem discretized over [a, b] and time-independent Schrödinger equation represented by a system of N+1 linear equations using a 3, 5 or 7 point stencil; N being the number of x-steps. Maximum value of N depends on device’s RAM: up to 4000 when computing eigenvalues and eigenvectors, up to 8000 when computing eigenvalues only.
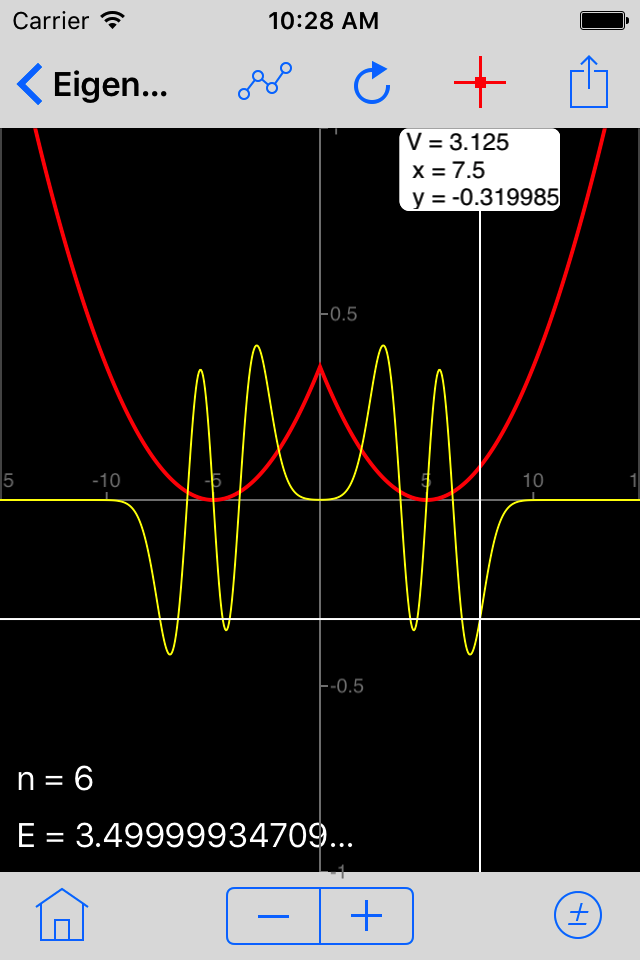
- Diagonalization of hamiltonian matrix H gives eigenvalues and eigenfunctions. When computing eigenvalues only, lowest energy levels of bound states (if any) with up to 10-digit precision.
- Listing of energy levels and visualisation of eigenwave-functions.
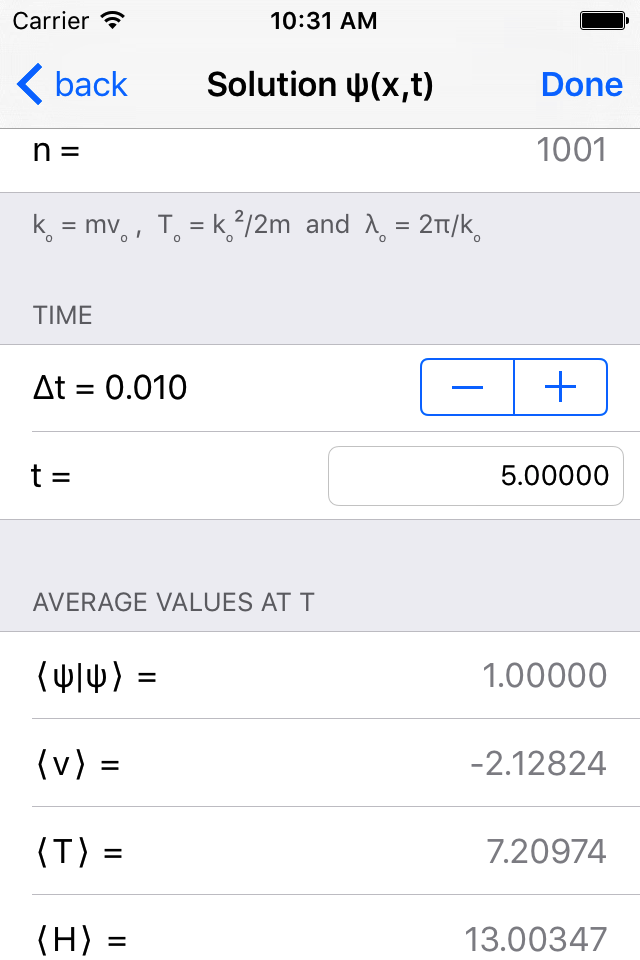
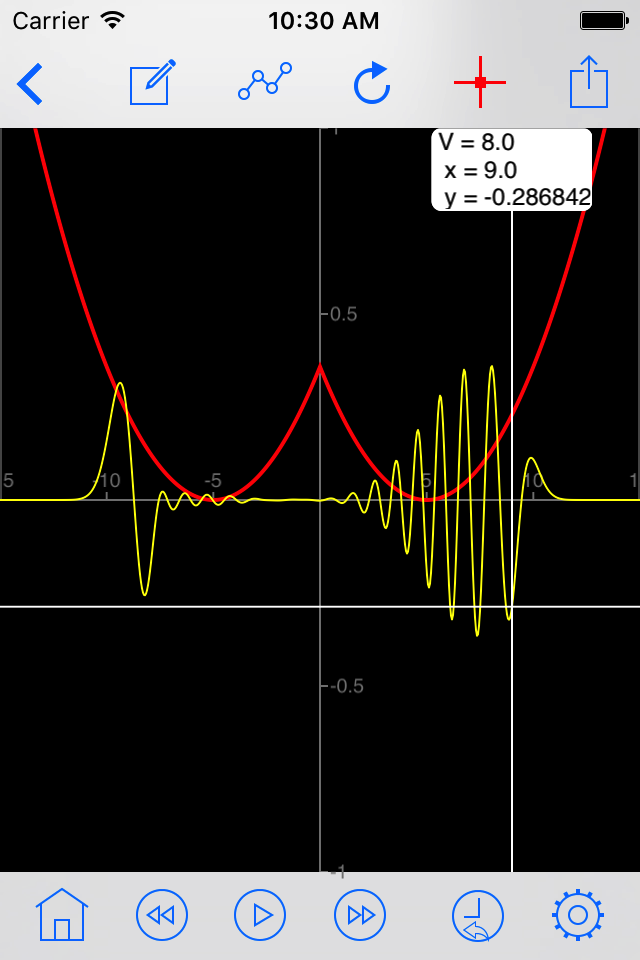
- Animation shows gaussian wave-packet ψ(x,t) evolving with real-time evaluation of average velocity, kinetic energy and total energy.
- Toggle between clockwise and counter-clockwise evolution of ψ(x,t).
- Watch Real ψ, Imag ψ or probability density |ψ|².
- Change initial gaussian parameters of the wave-packet (position, group velocity, standard deviation), enter any time value, then tap refresh button to observe changes in curves without new diagonalization. This is particularly useful to get a (usually more precise) solution for any time value t when animation is slower in cases of N being large.
- Watch both solution ψ(x,t) and free wave-packet curves evolve together in time and separate when entering non-zero potential energy region.
- Zoom in and out any part of the curves and watch how ψ(x,t) evolve locally.
Hide
Show More...
In Quantum Mechanics the one-dimensional Schrödinger equation is a fundamental academic though exciting subject of study for both students and teachers of Physics. A solution of this differential equation represents the motion of a non-relativistic particle in a potential energy field V(x). But very few solutions can be derived with a paper and pencil.
Have you ever dreamed of an App which would solve this equation (numerically) for each input of V(x) ?
Give you readily energy levels and wave-functions and let you see as an animation how evolves in time a gaussian wave-packet in this particular interaction field ?
Quantum Wave in a Box does it ! For a large range of values of the quantum system parameters.
Actually the originally continuous x-spatial differential problem is discretized over a finite interval (the Box) while time remains a continuous variable. The time-independent Schrödinger equation H ψ(x) = E ψ(x), represented by a set of linear equations, is solved by using quick diagonalization routines. The solution ψ(x,t) of the time-dependent Schrödinger equation is then computed as ψ(x,t) = exp(-iHt) ψ₀(x) where ψ₀(x) is a gaussian wave-packet at initial time t = 0.
You enter V(x) as RPN expression, set values of parameters and will get a solution in many cases within seconds !
- Atomic units used throughout (mass of electron = 1)
- Quantum system defined by mass, interval [a, b] representing the Box and (real) potential energy V(x).
- Spatially continuous problem discretized over [a, b] and time-independent Schrödinger equation represented by a system of N+1 linear equations using a 3, 5 or 7 point stencil; N being the number of x-steps. Maximum value of N depends on device’s RAM: up to 4000 when computing eigenvalues and eigenvectors, up to 8000 when computing eigenvalues only.
- Diagonalization of hamiltonian matrix H gives eigenvalues and eigenfunctions. When computing eigenvalues only, lowest energy levels of bound states (if any) with up to 10-digit precision.
- Listing of energy levels and visualisation of eigenwave-functions.
- Animation shows gaussian wave-packet ψ(x,t) evolving with real-time evaluation of average velocity, kinetic energy and total energy.
- Toggle between clockwise and counter-clockwise evolution of ψ(x,t).
- Watch Real ψ, Imag ψ or probability density |ψ|².
- Change initial gaussian parameters of the wave-packet (position, group velocity, standard deviation), enter any time value, then tap refresh button to observe changes in curves without new diagonalization. This is particularly useful to get a (usually more precise) solution for any time value t when animation is slower in cases of N being large.
- Watch both solution ψ(x,t) and free wave-packet curves evolve together in time and separate when entering non-zero potential energy region.
- Zoom in and out any part of the curves and watch how ψ(x,t) evolve locally.
Screenshots
Quantum Wave in a Box FAQ
-
Is Quantum Wave in a Box free?
Yes, Quantum Wave in a Box is completely free and it doesn't have any in-app purchases or subscriptions.
-
Is Quantum Wave in a Box legit?
Not enough reviews to make a reliable assessment. The app needs more user feedback.
Thanks for the vote -
How much does Quantum Wave in a Box cost?
Quantum Wave in a Box is free.
-
What is Quantum Wave in a Box revenue?
To get estimated revenue of Quantum Wave in a Box app and other AppStore insights you can sign up to AppTail Mobile Analytics Platform.

User Rating
App is not rated in South Africa yet.

Ratings History
Quantum Wave in a Box Reviews
Store Rankings

Ranking History
App Ranking History not available yet

Category Rankings
App is not ranked yet
Quantum Wave in a Box Competitors
| Name | Downloads (30d) | Monthly Revenue | Reviews | Ratings | Recent release | |
|---|---|---|---|---|---|---|
|
Quantum Mechanics - Theories
|
Unlock
|
Unlock
|
0
|
|
1 year ago | |
|
Waves: Partial Diff Eq
|
Unlock
|
Unlock
|
0
|
|
2 years ago | |
|
WaveAdd
|
Unlock
|
Unlock
|
0
|
|
3 years ago | |
|
Quantum Mechanics +
Solving Schrodinger's Equation
|
Unlock
|
Unlock
|
0
|
|
2 years ago | |
|
Kaemika
Chemical reactions simulator
|
Unlock
|
Unlock
|
0
|
|
3 years ago | |
|
ElectronOrbital
QuantumMechanicsWithYourEyes
|
Unlock
|
Unlock
|
0
|
|
1 year ago | |
|
ODE-Solver-Integrator
Integrate Solve Simulate Graph
|
Unlock
|
Unlock
|
0
|
|
1 week ago | |
|
EMwaveRT
|
Unlock
|
Unlock
|
0
|
|
1 year ago | |
|
Atomizer AR: Quantum Visuals
Proteins, Atomic Orbitals & MO
|
Unlock
|
Unlock
|
0
|
|
1 year ago | |
|
Epicycles
Experiment with Fourier series
|
Unlock
|
Unlock
|
0
|
|
1 year ago |
Quantum Wave in a Box Installs
Last 30 daysQuantum Wave in a Box Revenue
Last 30 daysQuantum Wave in a Box Revenue and Downloads
Gain valuable insights into Quantum Wave in a Box performance with our analytics.
Sign up now to access downloads, revenue, and more.
Sign up now to access downloads, revenue, and more.
App Info
- Category
- Education
- Publisher
- Michel Ramillon
- Languages
- English
- Recent release
- 1.0.3 (1 year ago )
- Released on
- Jan 1, 2017 (7 years ago )
- Also available in
- France , United States , Germany , Spain , United Kingdom , Malaysia , New Zealand , Norway , Netherlands , Nigeria , Philippines , Mexico , Latvia , Lebanon , Kazakhstan , Kuwait , South Korea , Peru , India , Pakistan , Poland , Romania , Russia , Saudi Arabia , Sweden , Singapore , Thailand , Türkiye , Taiwan , Ukraine , Vietnam , South Africa , Denmark , Argentina , Austria , Australia , Azerbaijan , Belgium , Brazil , Belarus , Canada , Switzerland , Chile , China , Colombia , Czechia , Japan , Dominican Republic , Algeria , Ecuador , Egypt , Finland , Greece , Hong Kong SAR China , Hungary , Indonesia , Ireland , Israel , United Arab Emirates , Italy
- Last Updated
- 3 days ago
This page includes copyrighted content from third parties, shared solely for commentary and research in accordance with fair use under applicable copyright laws. All trademarks, including product, service, and company names or logos, remain the property of their respective owners. Their use here falls under nominative fair use as outlined by trademark laws and does not suggest any affiliation with or endorsement by the trademark holders.