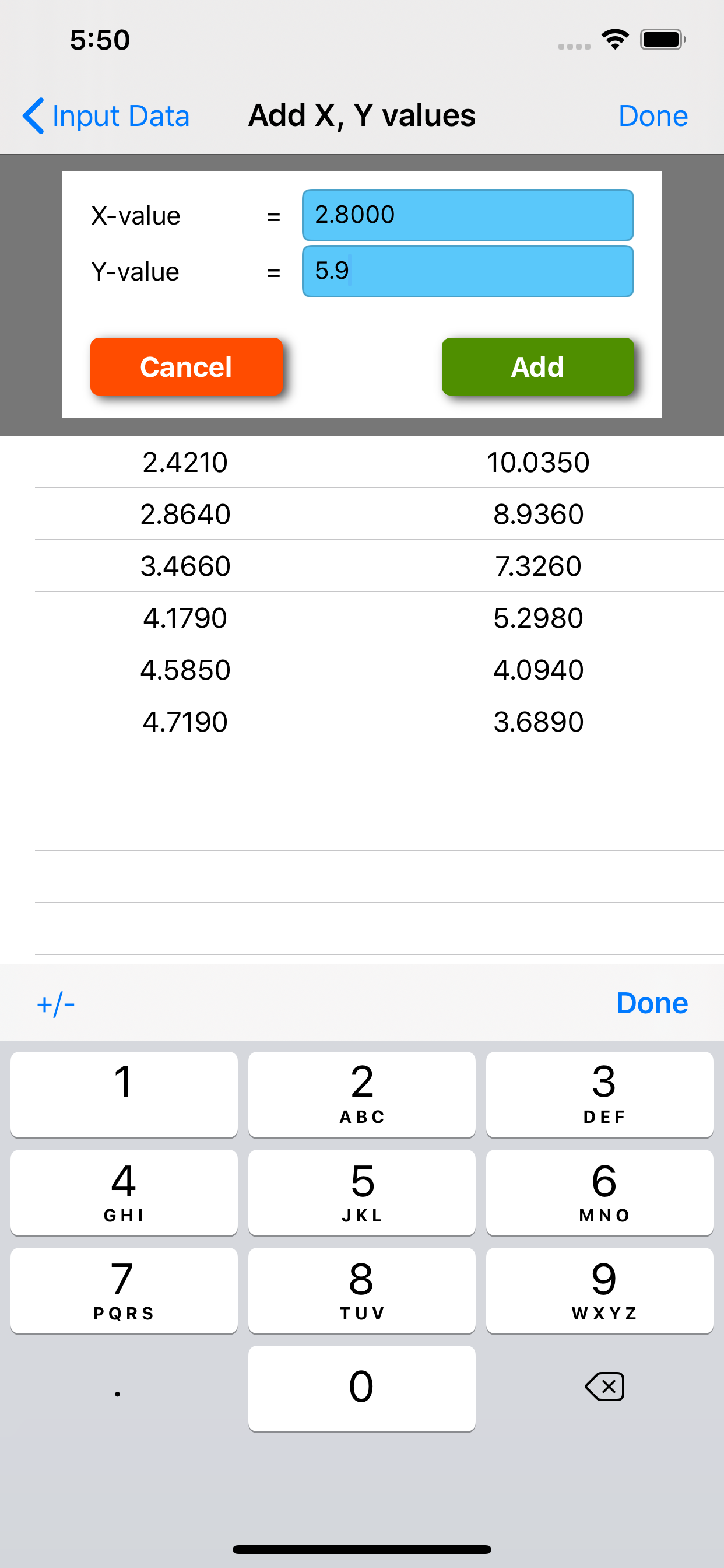
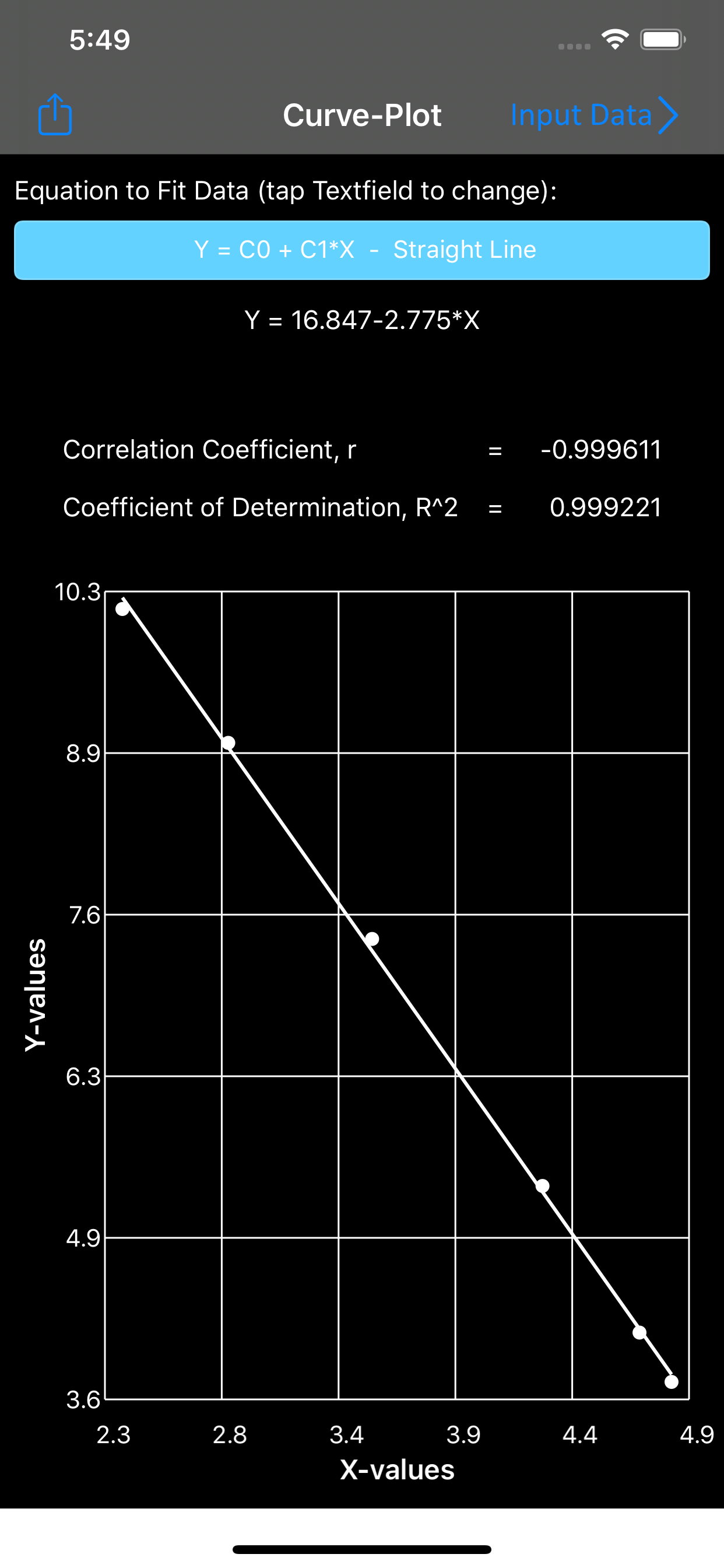
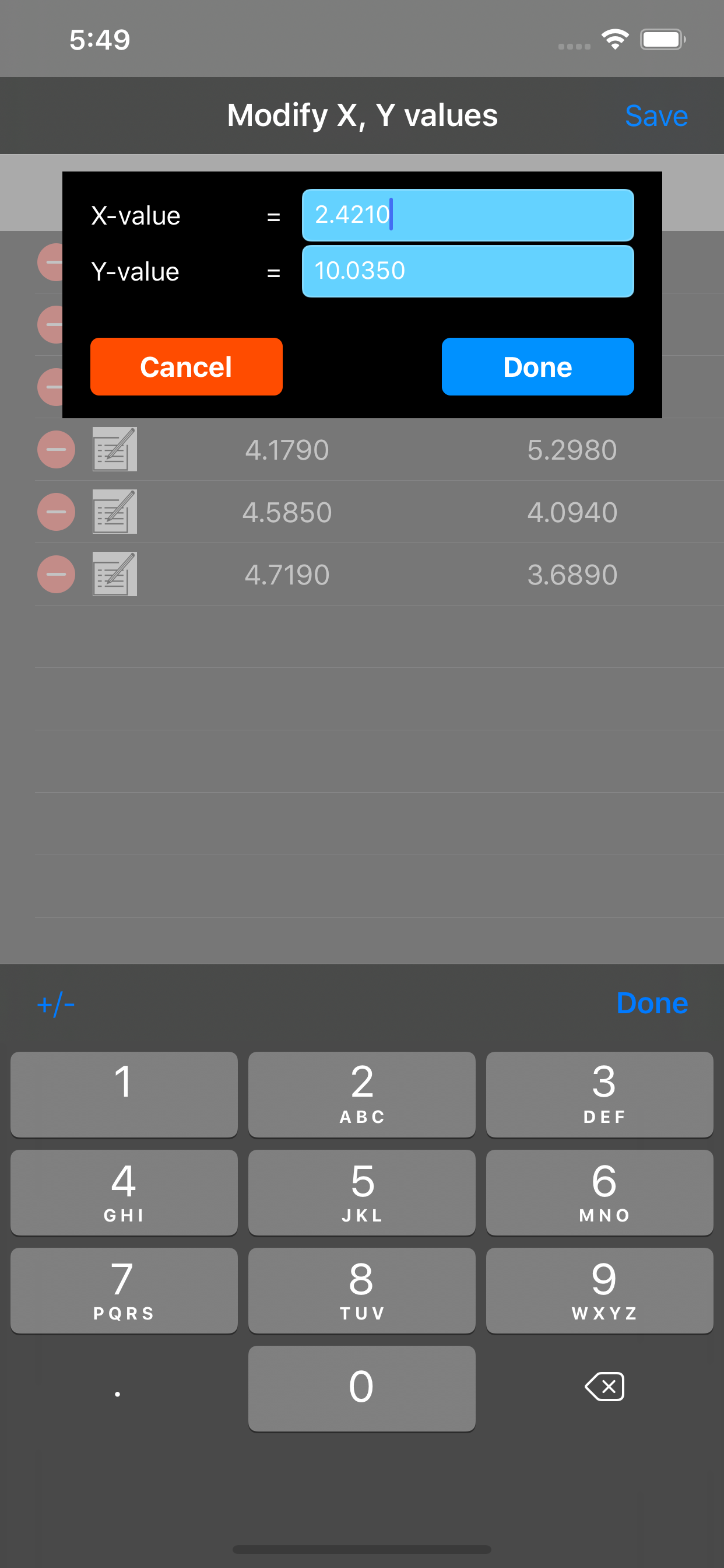
Beschreibung
'CurveFit' uses regression analysis by the method of least squares to find best fit for a set of data to a selected equation.
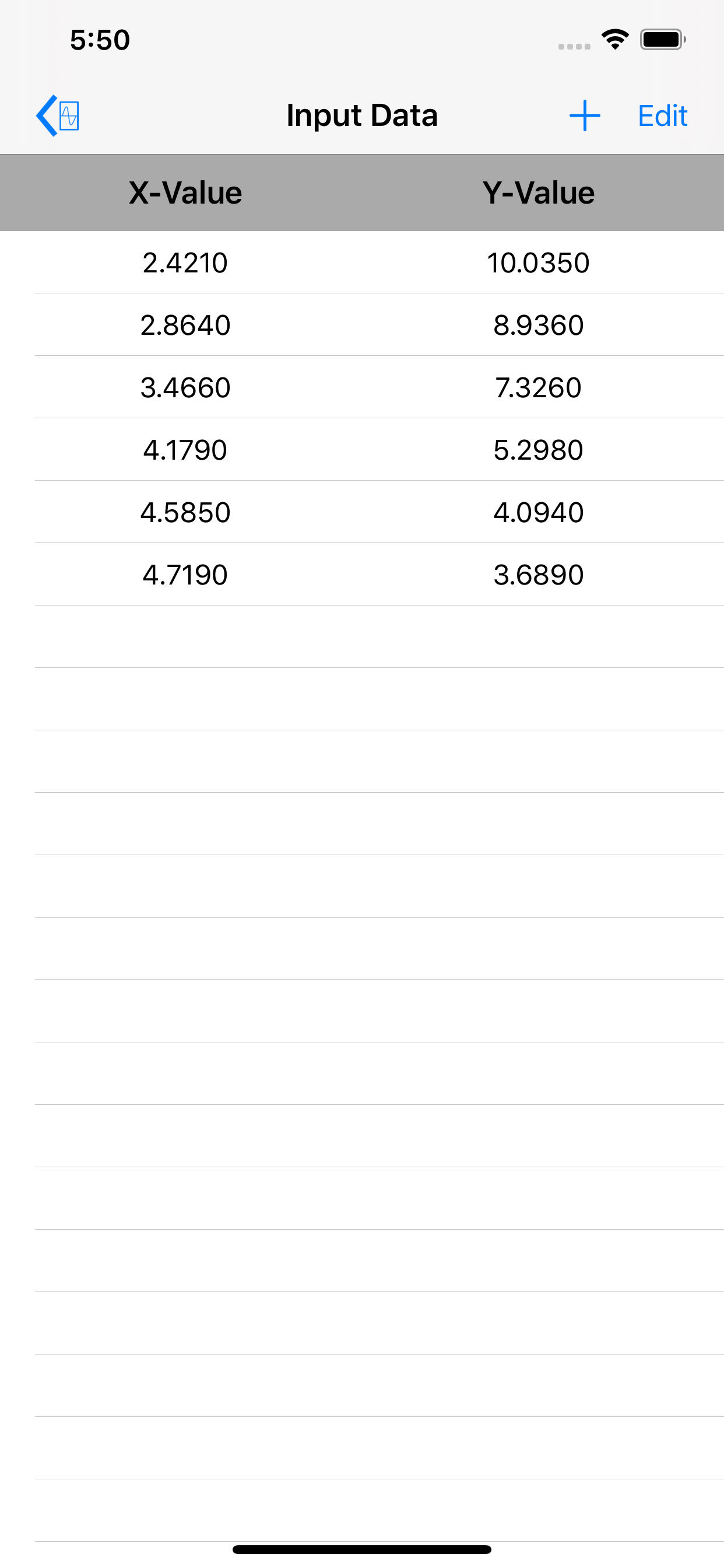
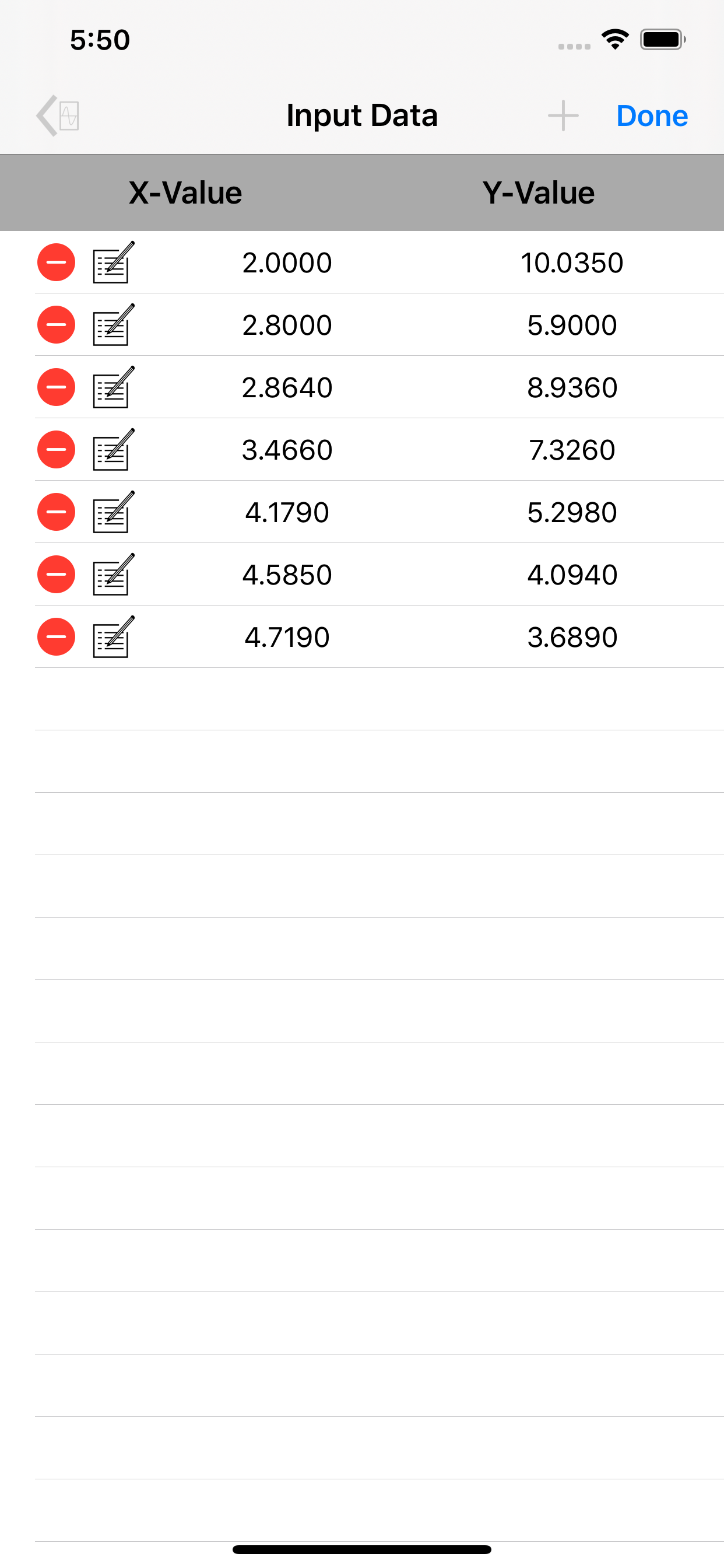
The curve-fitting technique used in this app is based on regression analysis by the method of least squares. The free version fits a straight line through a data-set using least squares analysis.
One In-App purchase is required to fit the other equations to the data set:
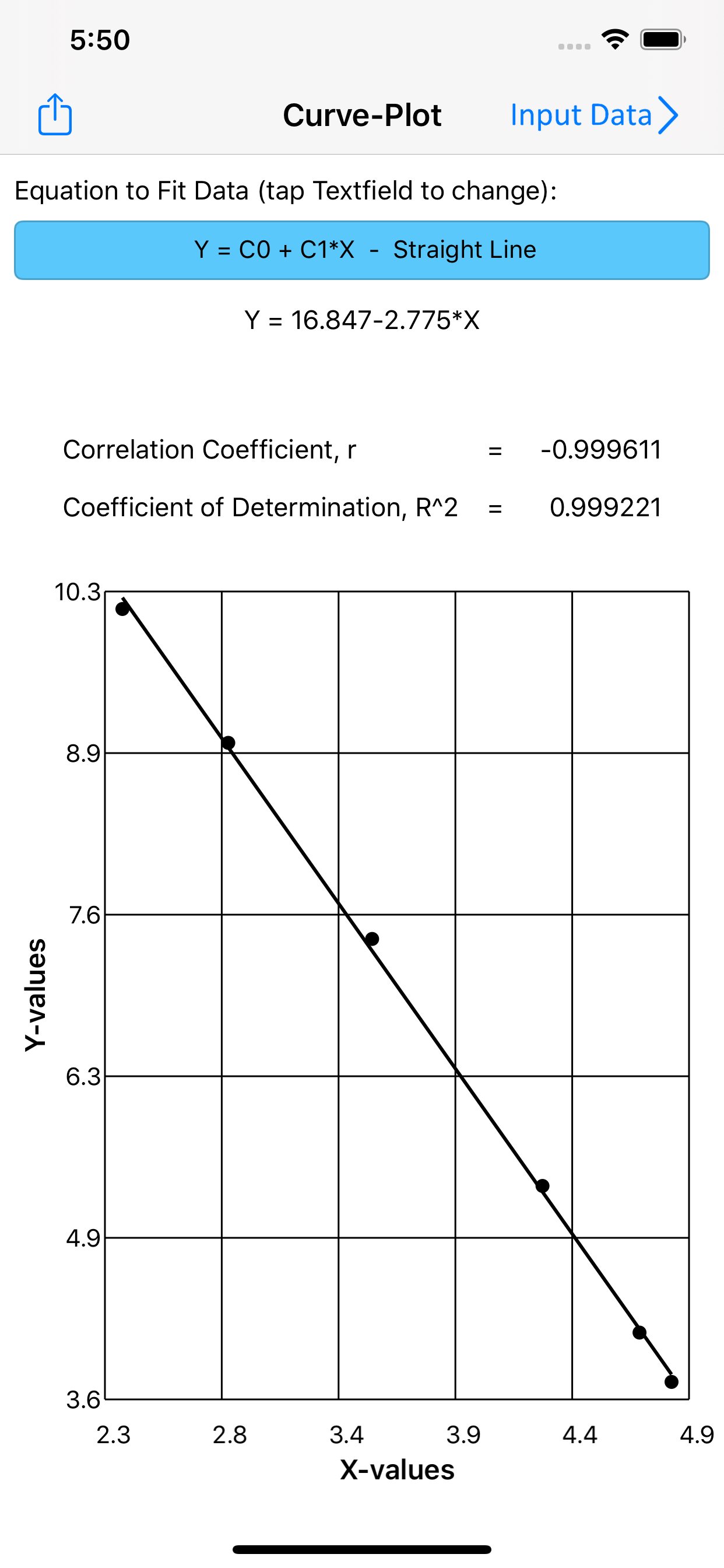
Straight Line : Y = C0 + C1*X (free)
Power Curve : Y = C0 + X^C1 Exponential I : Y = C0 * EXP(C1*X)
Exponential II : Y = C0 * X * EXP(C1*X)
Hyperbolic : Y = (C0 + C1*X)/(1 - C2*X)
Square Root : Y = C0 + C1*SQRT(X)
Polynomial : Y = C0 + C1*X + --- + CN*X^N
Exponential Poly : Y = C0 * EXP(C1*X + --- +
Natural Log : Y = C0 + C1*(LN(X)) + --- +
Reciprocal : Y = C0 + C1/X + --- + CN/X^N
Most literature deals with least squares analysis for straight lines, 2nd degree polynomials, and functions that can be linearized. The input-data is transformed into a format that the can be put into linear forms with undetermined constants. These types of equations are applicable for least-squares regression.
The regression routine is needed for determining values for the set of unknown quantities C1, C2,- - - ,Cm in the equation:
Y = C1 x F1(X) + C2 x F2(X) + - - - + Cm x Fm(X)
The constants are determined to minimize the sum of squares of the differences between the measured values (Y1, Y2, - - - , Yn) and the predicted equation Yc = F(X) which is found by curve-fitting the given data.
The principle of least squares is to find the values for the unknowns C1 through Cm that will minimize the sum of the squares of the residuals:
n
∑(ri) = r12 + r22 + - - - + rn2 = minimum
i=1
This is done by letting the derivative of the above equation equal zero. Thereby there will be generated as many algebraic equations as given data points, and the number of equations will be larger than unknowns.
Ausblenden
Mehr anzeigen...
The curve-fitting technique used in this app is based on regression analysis by the method of least squares. The free version fits a straight line through a data-set using least squares analysis.
One In-App purchase is required to fit the other equations to the data set:
Straight Line : Y = C0 + C1*X (free)
Power Curve : Y = C0 + X^C1 Exponential I : Y = C0 * EXP(C1*X)
Exponential II : Y = C0 * X * EXP(C1*X)
Hyperbolic : Y = (C0 + C1*X)/(1 - C2*X)
Square Root : Y = C0 + C1*SQRT(X)
Polynomial : Y = C0 + C1*X + --- + CN*X^N
Exponential Poly : Y = C0 * EXP(C1*X + --- +
Natural Log : Y = C0 + C1*(LN(X)) + --- +
Reciprocal : Y = C0 + C1/X + --- + CN/X^N
Most literature deals with least squares analysis for straight lines, 2nd degree polynomials, and functions that can be linearized. The input-data is transformed into a format that the can be put into linear forms with undetermined constants. These types of equations are applicable for least-squares regression.
The regression routine is needed for determining values for the set of unknown quantities C1, C2,- - - ,Cm in the equation:
Y = C1 x F1(X) + C2 x F2(X) + - - - + Cm x Fm(X)
The constants are determined to minimize the sum of squares of the differences between the measured values (Y1, Y2, - - - , Yn) and the predicted equation Yc = F(X) which is found by curve-fitting the given data.
The principle of least squares is to find the values for the unknowns C1 through Cm that will minimize the sum of the squares of the residuals:
n
∑(ri) = r12 + r22 + - - - + rn2 = minimum
i=1
This is done by letting the derivative of the above equation equal zero. Thereby there will be generated as many algebraic equations as given data points, and the number of equations will be larger than unknowns.
Screenshots
Curve-Fit Häufige Fragen
-
Ist Curve-Fit kostenlos?
Ja, Curve-Fit ist komplett kostenlos und enthält keine In-App-Käufe oder Abonnements.
-
Ist Curve-Fit seriös?
Nicht genügend Bewertungen, um eine zuverlässige Einschätzung vorzunehmen. Die App benötigt mehr Nutzerfeedback.
Danke für die Stimme -
Wie viel kostet Curve-Fit?
Curve-Fit ist kostenlos.
-
Wie hoch ist der Umsatz von Curve-Fit?
Um geschätzte Einnahmen der Curve-Fit-App und weitere AppStore-Einblicke zu erhalten, können Sie sich bei der AppTail Mobile Analytics Platform anmelden.

Benutzerbewertung
Die App ist in Deutschland noch nicht bewertet.

Bewertungsverlauf
Curve-Fit Bewertungen
Keine Bewertungen in Deutschland
Die App hat noch keine Bewertungen in Deutschland.
Store-Rankings

Ranking-Verlauf
App-Ranking-Verlauf noch nicht verfügbar

Kategorien-Rankings
App ist noch nicht gerankt
Curve-Fit Installationen
Letzte 30 TageCurve-Fit Umsatz
Letzte 30 TageCurve-Fit Einnahmen und Downloads
Gewinnen Sie wertvolle Einblicke in die Leistung von Curve-Fit mit unserer Analytik.
Melden Sie sich jetzt an, um Zugriff auf Downloads, Einnahmen und mehr zu erhalten.
Melden Sie sich jetzt an, um Zugriff auf Downloads, Einnahmen und mehr zu erhalten.
App-Informationen
- Kategorie
- Utilities
- Herausgeber
- Bjarne Berge
- Sprachen
- English
- Letzte Veröffentlichung
- 6.0 (vor 4 Jahren )
- Veröffentlicht am
- Feb 27, 2019 (vor 5 Jahren )
- Auch verfügbar in
- Taiwan, Vereinigte Staaten, Thailand, China, Litauen, Peru, Neuseeland, Norwegen, Niederlande, Nigeria, Malaysia, Mexiko, Polen, Libanon, Kasachstan, Kuwait, Südkorea, Japan, Philippinen, Pakistan, Indien, Portugal, Rumänien, Russland, Saudi-Arabien, Schweden, Singapur, Türkei, Ukraine, Vietnam, Südafrika, Dominikanische Republik, Argentinien, Österreich, Australien, Aserbaidschan, Belgien, Brasilien, Belarus, Kanada, Schweiz, Chile, Kolumbien, Tschechien, Deutschland, Dänemark, Italien, Algerien, Ecuador, Ägypten, Spanien, Finnland, Frankreich, Vereinigtes Königreich, Griechenland, Sonderverwaltungsregion Hongkong, Ungarn, Indonesien, Irland, Israel, Vereinigte Arabische Emirate
- Zuletzt aktualisiert
- vor 3 Wochen
This page includes copyrighted content from third parties, shared solely for commentary and research in accordance with fair use under applicable copyright laws. All trademarks, including product, service, and company names or logos, remain the property of their respective owners. Their use here falls under nominative fair use as outlined by trademark laws and does not suggest any affiliation with or endorsement by the trademark holders.
- © 2025 AppTail.
- Unterstützung
- Privacy
- Terms
- All Apps