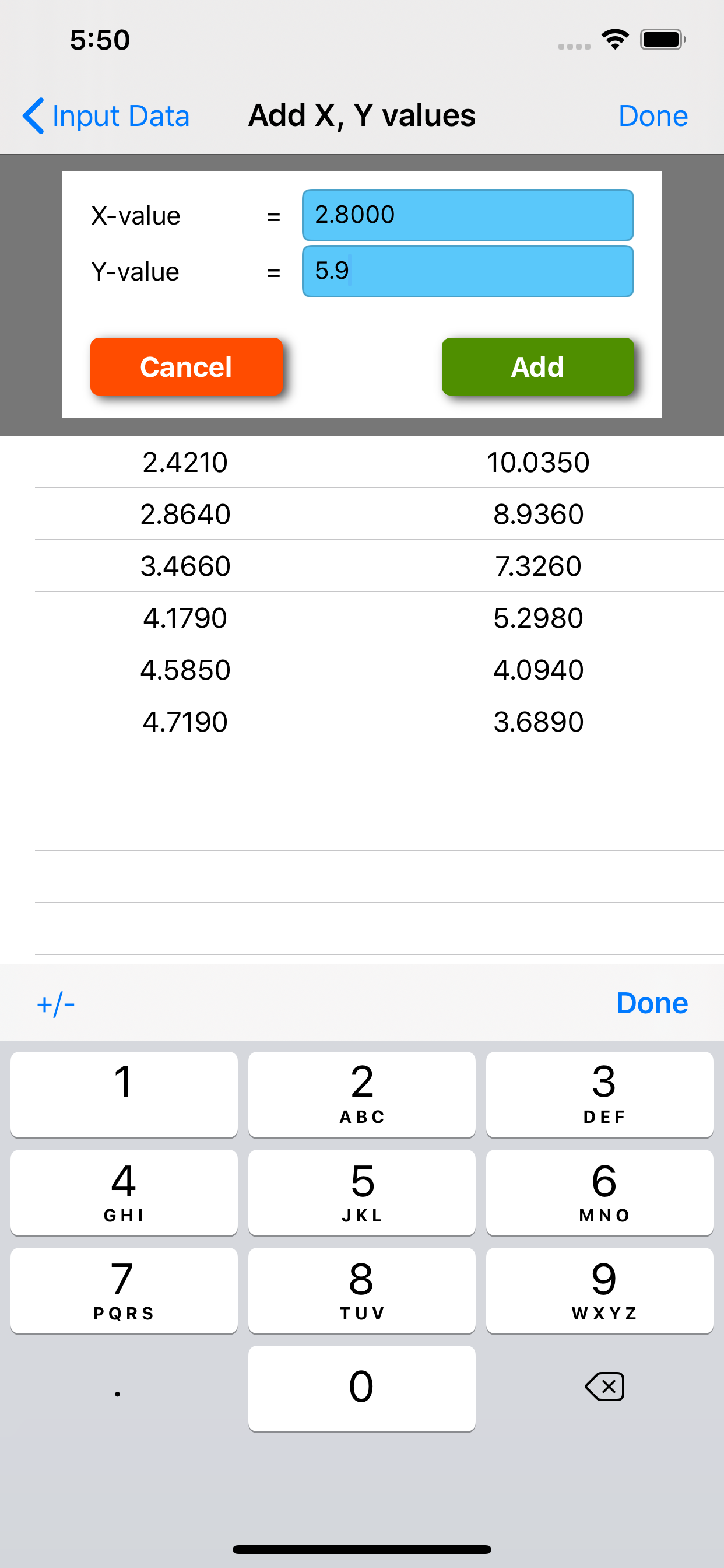
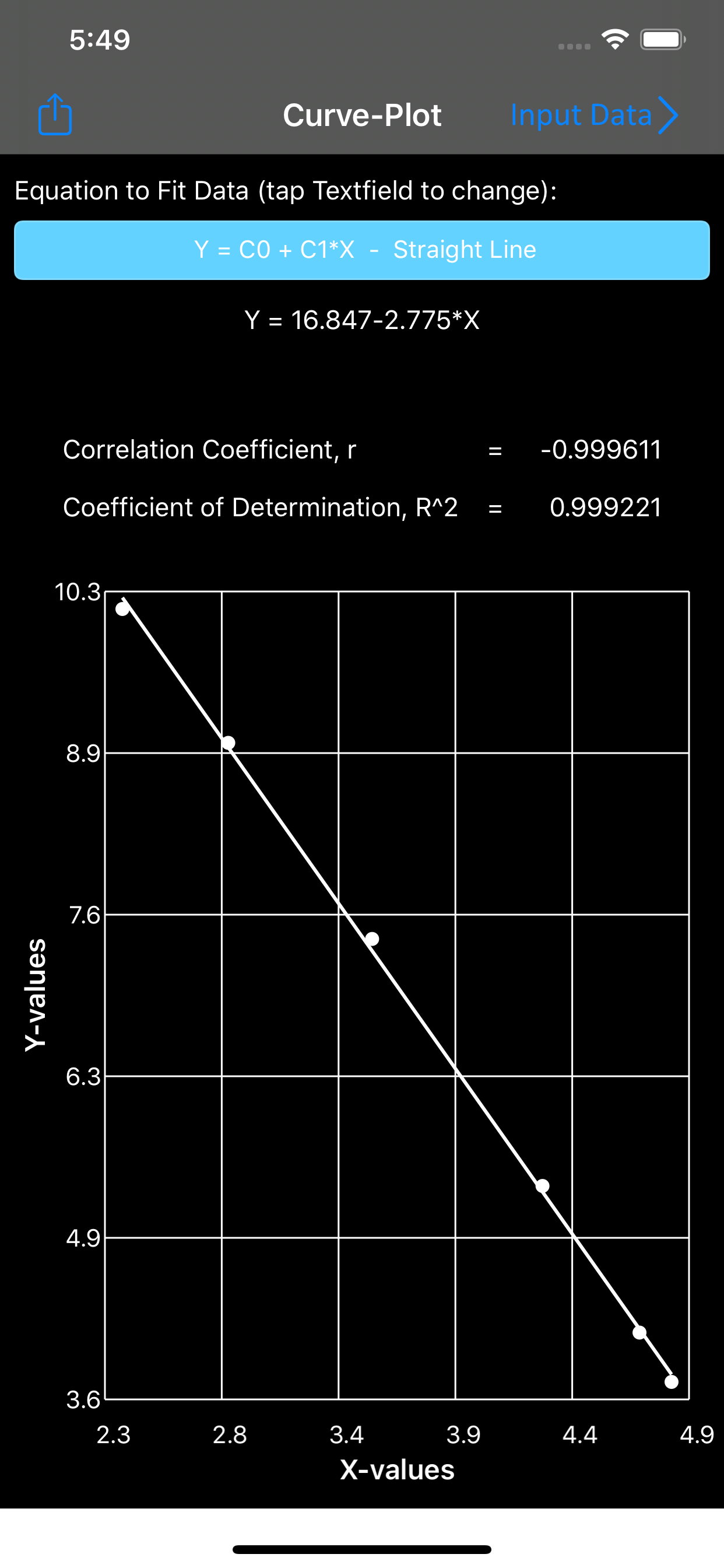
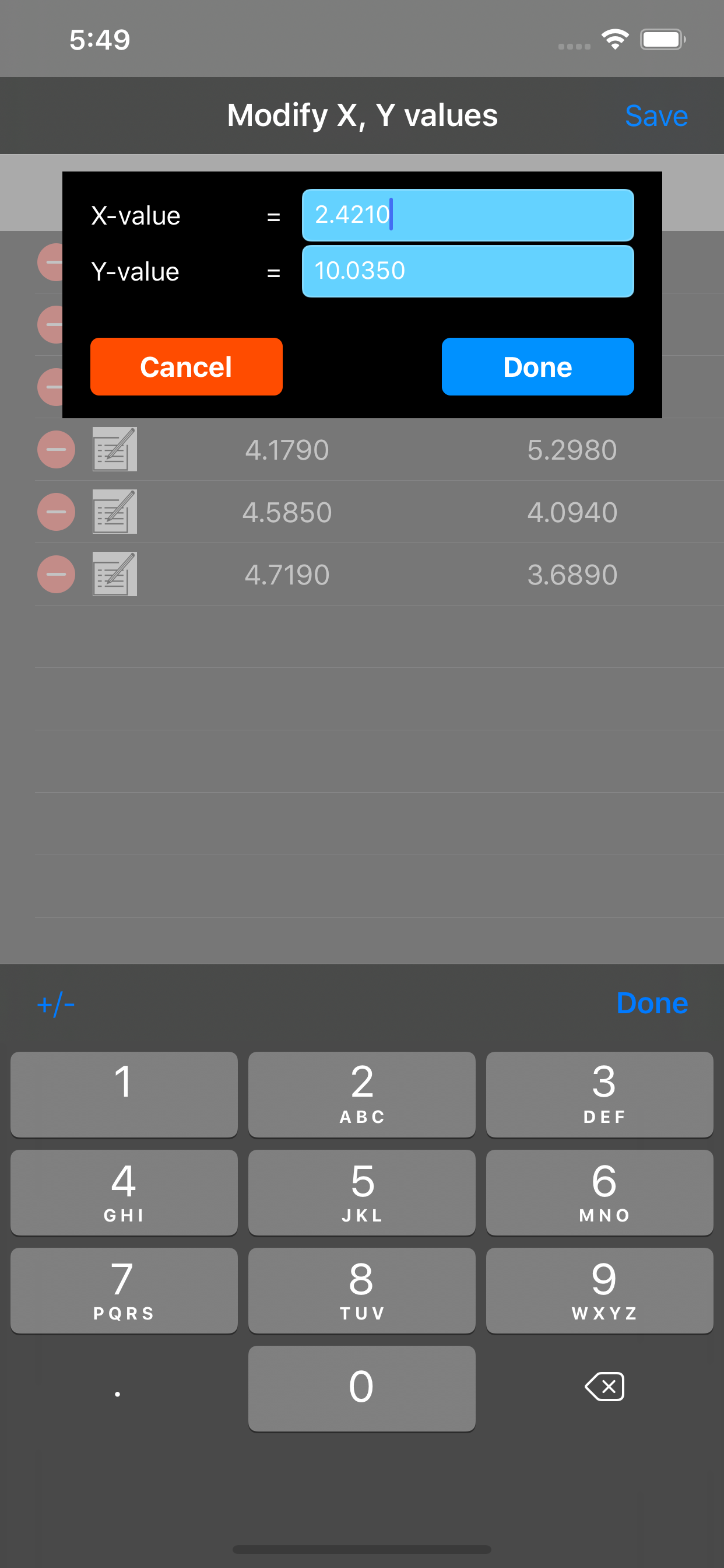
Описание
'CurveFit' uses regression analysis by the method of least squares to find best fit for a set of data to a selected equation.
The curve-fitting technique used in this app is based on regression analysis by the method of least squares. The free version fits a straight line through a data-set using least squares analysis.
One In-App purchase is required to fit the other equations to the data set:
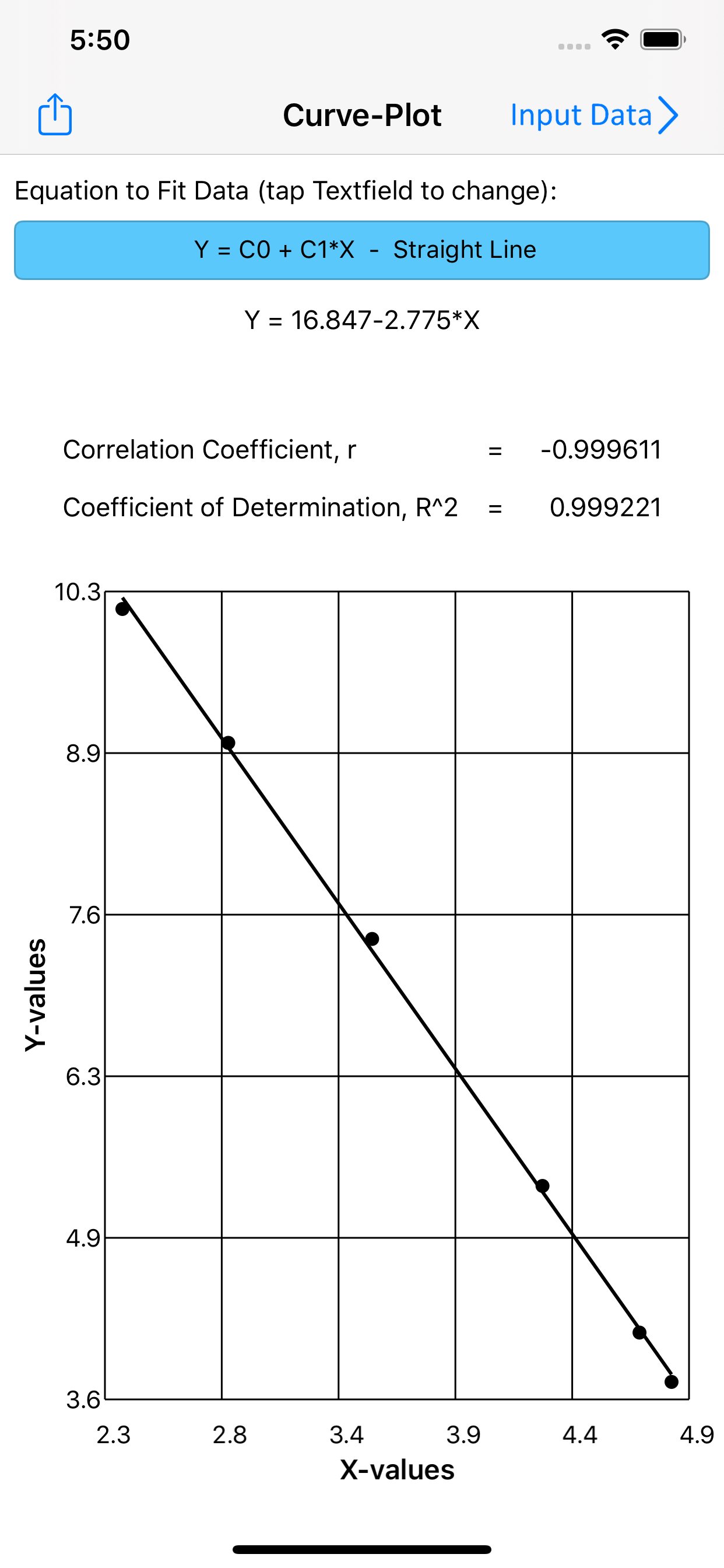
Straight Line : Y = C0 + C1*X (free)
Power Curve : Y = C0 + X^C1 Exponential I : Y = C0 * EXP(C1*X)
Exponential II : Y = C0 * X * EXP(C1*X)
Hyperbolic : Y = (C0 + C1*X)/(1 - C2*X)
Square Root : Y = C0 + C1*SQRT(X)
Polynomial : Y = C0 + C1*X + --- + CN*X^N
Exponential Poly : Y = C0 * EXP(C1*X + --- +
Natural Log : Y = C0 + C1*(LN(X)) + --- +
Reciprocal : Y = C0 + C1/X + --- + CN/X^N
Most literature deals with least squares analysis for straight lines, 2nd degree polynomials, and functions that can be linearized. The input-data is transformed into a format that the can be put into linear forms with undetermined constants. These types of equations are applicable for least-squares regression.
The regression routine is needed for determining values for the set of unknown quantities C1, C2,- - - ,Cm in the equation:
Y = C1 x F1(X) + C2 x F2(X) + - - - + Cm x Fm(X)
The constants are determined to minimize the sum of squares of the differences between the measured values (Y1, Y2, - - - , Yn) and the predicted equation Yc = F(X) which is found by curve-fitting the given data.
The principle of least squares is to find the values for the unknowns C1 through Cm that will minimize the sum of the squares of the residuals:
n
∑(ri) = r12 + r22 + - - - + rn2 = minimum
i=1
This is done by letting the derivative of the above equation equal zero. Thereby there will be generated as many algebraic equations as given data points, and the number of equations will be larger than unknowns.
Скрыть
Показать больше...
The curve-fitting technique used in this app is based on regression analysis by the method of least squares. The free version fits a straight line through a data-set using least squares analysis.
One In-App purchase is required to fit the other equations to the data set:
Straight Line : Y = C0 + C1*X (free)
Power Curve : Y = C0 + X^C1 Exponential I : Y = C0 * EXP(C1*X)
Exponential II : Y = C0 * X * EXP(C1*X)
Hyperbolic : Y = (C0 + C1*X)/(1 - C2*X)
Square Root : Y = C0 + C1*SQRT(X)
Polynomial : Y = C0 + C1*X + --- + CN*X^N
Exponential Poly : Y = C0 * EXP(C1*X + --- +
Natural Log : Y = C0 + C1*(LN(X)) + --- +
Reciprocal : Y = C0 + C1/X + --- + CN/X^N
Most literature deals with least squares analysis for straight lines, 2nd degree polynomials, and functions that can be linearized. The input-data is transformed into a format that the can be put into linear forms with undetermined constants. These types of equations are applicable for least-squares regression.
The regression routine is needed for determining values for the set of unknown quantities C1, C2,- - - ,Cm in the equation:
Y = C1 x F1(X) + C2 x F2(X) + - - - + Cm x Fm(X)
The constants are determined to minimize the sum of squares of the differences between the measured values (Y1, Y2, - - - , Yn) and the predicted equation Yc = F(X) which is found by curve-fitting the given data.
The principle of least squares is to find the values for the unknowns C1 through Cm that will minimize the sum of the squares of the residuals:
n
∑(ri) = r12 + r22 + - - - + rn2 = minimum
i=1
This is done by letting the derivative of the above equation equal zero. Thereby there will be generated as many algebraic equations as given data points, and the number of equations will be larger than unknowns.
Встроенные покупки
- Curve-Fit
- ₹299.00
Скриншоты
Curve-Fit Частые Вопросы
-
Приложение Curve-Fit бесплатное?
Да, Curve-Fit можно скачать бесплатно, однако в приложении есть встроенные покупки или подписки.
-
Является ли Curve-Fit фейковым или мошенническим?
Недостаточно отзывов для надежной оценки. Приложению нужно больше отзывов пользователей.
Спасибо за ваш голос -
Сколько стоит Curve-Fit?
Curve-Fit имеет несколько покупок/подписок внутри приложения, средняя цена покупки составляет ₹299.00.
-
Сколько зарабатывает Curve-Fit?
Чтобы получить оценку дохода приложения Curve-Fit и другие данные AppStore, вы можете зарегистрироваться на платформе мобильной аналитики AppTail.

Оценки пользователей
Приложение еще не оценено в Индия.

История оценок
Curve-Fit Отзывы Пользователей
Оценки

История позиций в топах
История рейтингов пока не доступна

Позиции в категории
Приложение еще не было в топах
Ключевые слова
Curve-Fit Конкуренты
Curve-Fit Установки
30дн.Curve-Fit Доход
30дн.Curve-Fit Доходы и Загрузки
Получите ценные инсайты о производительности Curve-Fit с помощью нашей аналитики.
Зарегистрируйтесь сейчас, чтобы получить доступ к статистика загрузок и доходов и многому другому.
Зарегистрируйтесь сейчас, чтобы получить доступ к статистика загрузок и доходов и многому другому.
Информация о приложении
- Категория
- Utilities
- Разработчик
- Bjarne Berge
- Языки
- English
- Последнее обновление
- 6.0 (4 года назад )
- Выпущено
- Feb 27, 2019 (5 лет назад )
- Также доступно в
- Тайвань , Соединенные Штаты , Таиланд , Китай , Литва , Перу , Новая Зеландия , Норвегия , Нидерланды , Нигерия , Малайзия , Мексика , Польша , Ливан , Казахстан , Кувейт , Республика Корея , Япония , Филиппины , Пакистан , Индия , Португалия , Румыния , Россия , Саудовская Аравия , Швеция , Сингапур , Турция , Украина , Вьетнам , Южно-Африканская Республика , Доминиканская Республика , Аргентина , Австрия , Австралия , Азербайджан , Бельгия , Бразилия , Беларусь , Канада , Швейцария , Чили , Колумбия , Чехия , Германия , Дания , Италия , Алжир , Эквадор , Египет , Испания , Финляндия , Франция , Великобритания , Греция , Гонконг (САР) , Венгрия , Индонезия , Ирландия , Израиль , ОАЭ
- Обновлено
- 8 часов назад
This page includes copyrighted content from third parties, shared solely for commentary and research in accordance with fair use under applicable copyright laws. All trademarks, including product, service, and company names or logos, remain the property of their respective owners. Their use here falls under nominative fair use as outlined by trademark laws and does not suggest any affiliation with or endorsement by the trademark holders.
AppTail.